4.2 基本解とロンスキアン
この節では、ロンスキアン を使って、3章2節と同様の結果が
1階の変数係数連立微分方等式 に対しても成り立つことを示す。
簡単のため、2未知変数の場合を考える。
つぎの斉次連立微分方程式を考える。
(4.21) y1' = a11 (x)y1 + a12 (x)y2
y2' = a21 (x)y1 + a22 (x)y2
ここで、 aij (x) (i, j =1, 2) は 区間 I 上の連続関数とする。
(4.21) のベクトル表示を与えよう。
この事から、 |W(x)| は 区間 I 上で恒等的に 0 か または決して 0 にならない事
がわかる。|W(x)| ≠ 0, x ∈ I のとき、 つまり W(x) が I 上で正則のとき、
y1, y2 は I 上 で独立になる。 このとき、 W(x) を (4.21) または (4.22) の
基本解 もしくは、 解の基本形系 という。
確かめよう。
このとき、共に 0 でない定数 C1, C2 をとって、 C1 y1(x0) + C2 y2(x0) = 0
とできる。
今 y = C1 y1 + C2 y2 とおくと 、 y' = A(x)y かつ y(x0) = 0 より、
初期値問題の解の一意性(次章で説明)から y(x) = 0, ∀x∈I となり、
C1 y1 + C2 y2 ≡ 0 がいえるので y1, y2 は一次従属。
さて、 y1, y2 を (4.22) の基本解とする。
(存在については、|W(x0)| ≠ 0, ∃x0 ∈ I なるものを選べばよい)
さらに y を (4.22) の勝手な解とする。 このとき |W(x)| ≠ 0, x ∈ I であるから、
行列式論の クラーメルの公式 により I 上の関数 c₁(x), c₂(x) で、
(4.24) c₁(x) y₁+ c₂(x) y₂ = y
となるものが存在する。 c₁(x), c₂(x) が微分可能なことは、明らかだろう。
(4.24) を微分して (4.22) を使うと、
(4.25) A(x) y = y' = c₁(x) y₁' + c₂(x) y₂' + c₁'(x) y₁+ c₂'(x) y₂
= c₁(x) A(x)y₁ + c₂(x)A(x) y₂ + c₁'(x) y₁+ c₂'(x) y₂
= A(x)( c₁(x) y₁ + c₂(x) y₂) + c₁'(x) y₁ + c₂'(x) y₂
= A(x)y + c₁'(x) y₁ + c₂'(x) y₂
よって
(4.26) c₁'(x) y₁ + c₂'(x) y₂= 0
がしたがう。 ここで、 y1, y2 は一次独立であったから、
c₁'(x) ≡ 0, c₂'(x) ≡ 0
となり、 c₁(x) = C1, c₂= C2, ( C1, C2 は定数) となる。 すなわち、
(4.27) y = C1 y₁+ C2 y₂
と書ける。 すなわち、次の定理がなりたつ。
定数変化公式
次にロンスキアン W(x) = W[y1, y2 ](x) を用いて 非斉次方程式
(4.28) y' = A(x) y + f (x), f (x) = (f1(x), f2(x))t
の一般解を定数変化法を用いて 3章2節と同様にして求めよう。
(4.29) y = c₁(x) y₁+ c₂(x) y₂
の形で (4.28) の解を求めよう。 (4.29) を微分して (4.28) を使うと、先と同様の計算により
y' = c₁(x) y₁' + c₂(x) y₂' + c₁'(x) y₁ + c₂'(x) y₂
= c₁(x) A(x)y₁ + c₂(x) A(x)y₂ + c₁'(x) y₁ + c₂'(x) y₂
= A(x)y + c₁'(x) y₁ + c₂'(x) y₂
= A(x)y + f (x)
となり、最後の2式より
(4.30) c₁'(x) y₁ + c₂'(x) y₂ = f (x)
がしたがう。 よって クラメールの公式により
4.3 高階の微分方程式と連立微分方程式
ここでは、単独の n階微分方程式を連立微分方程式に直すことを考える。
(4.31) y(n) + a1(x)y(n-1) + ・・・ + an(x)y = f(x)
に対し
(4.32) y1 = y, y2 = y(1), ・・・・ , yn = y(n-1)
とおくと、 y = (y1, y2, ・・・・ , yn )t に対する
ベクトル微分方程式
一般に、 A(x) を n×n 行列関数として、 n未知変数の連立微分方程式
(4.34) y' = A(x)y + f(x)
を考えよう。 (4.34) の斉次形 y' = A(x)y の n個の解
y1 , y2 , ・・・・ , yn に対し
(4.34) の ロンスキアン W(x) = W[ y1 , y2 , ・・・・ , yn](x) を
行列式 |(y1, y2, ・・・・ , yn )| により定義する。
この定義の下で、 (4.32) より (4.31) に対するロンスキアン と
(4.33) に対するロンスキアンは一致することがわかる。
このように、連立一次微分方程式を考察することは、
高階の微分方程式を考察することにつながる。



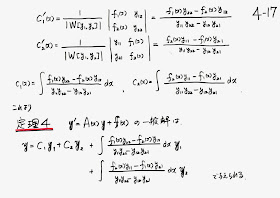



0 件のコメント:
コメントを投稿