3. 現代数学
現代数学(もしくは 高等数学) は、
純粋数学 と 応用数学
にわけられます。
実は、厳密に分けられるという事ではありません。 便宜的にです。
純粋数学 には、 つぎの分野があります。
代数学
幾何学
解析学
集合論
応用数学 には、 つぎの分野があります。
計算科学
確率論
統計学
それぞれの分野には、さらに扱う対象によって色々な分野わけができます。
といった具合です。
様々な研究分野があるということが解れば十分です。
4. 数学は美しい
ここでは、 数学の構造の中にある美しさと、
それを用いた芸術家の作品についてみていきましょう。
4.1. 数学的フォルムを用いた杉本博司の作品 と ディ二曲面
写真家の杉本博司(すぎもと ひろし)は、数学的形態 ということで、
様々な曲面の石膏像写真を撮っています。
紹介します。
2次曲面や、ディ二曲面が現れています。
次のような、球体を含む写真もあります。
著作権の関係があるので、これだけにします。
ディ二曲面 とは、擬球を捩じってえられる負の低曲率曲面です。
何のことかわからないと思いますので、無視してください。
幾つかの画像でディ二曲面 をたのしみましょう。
機能的な美しさがありますね。
4.2. オイラーと多面体
皆さんは、オイラーはよくご存じですね。 盲目の数学者として有名です。
レオンハルト・オイラー(Leonhard Euler, 1707年4月15日 - 1783年9月18日)
オイラー は数学者 かつ物理学者であり、天文学者でもあります。
微積分成立以後の18世紀の数学の中心となって、続く19世紀の厳密化・抽象化時代の礎を
築いたとされる。
膨大な研究業績があり、その全集出版はいまだ完成されていないそうです。
オイラーで有名なのは、
オイラーの多面体定理
でしょう。 すべての多面体について、
- 頂点の数 - 辺の数 + 面の数 = 2
多面体には、こんなのがあります。 定理を確かめてください。
そのほかにも、
面白そうな多面体が沢山あります。
折り紙で作った多面体
穴あき多面体
穴の開いている多面体に関しては、オイラーの多面体定理 は成り立ちません。
木で組み立てられたスケルトン多面体もあります。
トランプのカードでも・・・
傑作なのは、こんな多面体のお家に住んでいる人がいることです。
4.3. エッシャーによる数学的芸術
マウリッツ・コルネリス・エッシャー
(Maurits Cornelis Escher, 1898年6月17日 - 1972年3月27日)
は版画製作でよく知られたオランダの画家(版画家)です。
建築不可能な構造物や、無限を有限のなかに閉じ込めたもの、
平面を次々と変化するパターンで埋め尽くしたもの、
など非常に独創的な作品を作り上げた。
数学的には、繰り返し変形パターンや不可能構造の視覚化を実現した
異能の芸術家といえるでしょう。
彼の作品を見ていきましょう。
勧められました。 これには繰り返し模様に関する論文が掲載されており、
平面を同じ図形で埋める方法(平面充填)の研究が創作の刺激になっています。
彼の有名な、リトグラフ(石版画)を挙げていきましょう。
 立体的には、不可能です。 トリックアートの祖先ですね。
立体的には、不可能です。 トリックアートの祖先ですね。
Escherの公式サイト もあります。 ご覧になってください。
ブノワ・マンデルブロ
(Benoît B. Mandelbrot, 1924年11月20日 - 2010年10月14日)
はユダヤ人でフランス系アメリカ人の数学者であり、経済学者であり、自然科学者。
フラクタルの父として著名である。
彼の有名なことばに、
Fractal is Everywhere.
というのがあります。 フラクタルは、どこでも ですね。
マンデルブロ集合(Mandelbrot set)とは、
複素平面上の集合、またはそれを複素平面上にプロットしたフラクタル図形。
詳しくは、

満たす複素数 c 全体が作る集合がマンデルブロ集合である。
この黒い点の集合です。
マンデルブロ集合 にあるズーム動画を是非見てください。
実に様々な形態が生じることがわかります。
YouTube にもあります。 こちらのほうが綺麗です。
拡大イメージ
 全体図 |  拡大 1 |  拡大 2 |  拡大 3 |  拡大 4 |
 拡大 5 |  拡大 6 |  拡大 7 |  拡大 8 |  拡大 9 |
 拡大 10 |  拡大 11 |  拡大 12 |  拡大 13 |  拡大 14 |
こんな風です。
簡単な式から、こんなに多様な図形が現れるのは神秘的ですね。
私も、20年位前に 簡単なBasicのプログラムで、フラクタル図形を描かせたことがあります。
その頃は、1枚の絵を描くのに1日がかりで計算機を走らせていました。
フラクタルの静止画像を幾つかピックアップします。
まづは、Koch図形です。
このようにして、雪の結晶ができます。
変形したものを含め色々見ていきましょう。
つぎは、マンデルブロ図形です。
ジュリア集合とは
初期値 z0 を与える集合である。
こちらのほうも、幾つか画像を与えよう。
同じ図形がありますが、色づけで変わってみえますね。
フラクタル図形を利用したアート作品があります。
幻想的な絵ですね。 人間の絵筆では、ちょっと描けません。
切りがないので、ここで小休止します。
To Be Continued
今回は、沢山書いた(コピペした?)ので次回で終わります。















































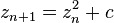
.jpg)






.jpg)














0 件のコメント:
コメントを投稿